---

1 2 3 4 5

Leyes de Kepler

Primera: Cada planeta en su movimiento describe una elipse, en uno de cuyos focos se encuentra el Sol

bservando Marte, Kepler comprobó que giraba alrededor del Sol siguiendo una elipse en lugar de un circunferencia.

La circunstancia de que fuera Marte y no otro planeta del Sistema Solar el observado, fue una fortuita coincidencia, pues Marte posee la órbita más elíptica en comparación con los demás planetas. Si hubiera estudiado, por ejemplo a Venus, Kepler nunca habría descubierto las verdaderas órbitas de los planetas.

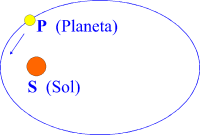
Primera ley de Kepler: Un planeta (P) se mueve siguiendo una elipse con el Sol (S) en uno de sus focos

En las órbitas elípticas el Sol nunca está en el centro, sino que se encuentra desplazado en un foco de la elipse. Se puede decir que los planetas "caen hacia el Sol", pues cuando uno de ellos que siga una órbita elíptica se encuentra próximo al Sol, se acelera. Por el contrario, va más lento cuando está en el punto más alejado de él.

Segunda: Las áreas barridas por el radio vector que une un planeta con el Sol, son iguales en tiempos iguales

Si un cuerpo realiza un movimiento circular uniforme, recorrerá en tiempos iguales un ángulo igual o una fracción igual del arco del círculo.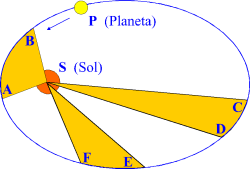

Segunda ley de Kepler: Un planeta barre áreas iguales en tiempos iguales. El tiempo que necesita el planeta Ppara ir de Ba Aes el mismo que necesita para ir de Fa Ey de Da C; las áreas sombreadas que barre BSA, FSEy DSC son iguales

En una circunferencia se precisa doble tiempo para recorrer dos terceras partes, que para recorrer solamente un tercio de ella. Sin embargo, Kepler descubrió que en una órbita elíptica no se cumplía esta característica. Así, por ejemplo, un planeta al moverse a lo largo de la elipse en su órbita alrededor del Sol, cuando se encuentra próximo a él, traza en un periodo de tiempo dado un arco grande, sin embargo el área de ese arco es pequeña precisamente por su proximidad al Sol. Al contrario, cuando el planeta se encuentra alejado del Sol, para el mismo periodo de tiempo cubre un arco mucho más pequeño, pero que corresponde a un área mayor por encontrarse el Sol más distante. Pues bien, Kepler descubrió que tanto el área mayor (cuando está lejos del Sol), como la menor (cuando está más próximo) eran exactamente iguales, independientemente de lo elíptica que fuera la órbita.

Tercera: Los cuadrados de los períodos de revolución, es decir, los tiempos empleados por cada planeta en describir una órbita completa, son proporcionales a los cubos de los semiejes mayores de las órbitas, o sea a los cubos de sus distancias medias al Sol

Años después de que Kepler enunciara sus dos primeras leyes, descubrió su tercera y última ley o ley armónica. Ésta relaciona entre sí el tamaño de la órbita de un planeta y el periodo necesario para dar una vuelta alrededor del Sol.

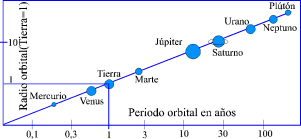
La tercera ley de Kepler, o ley armónica, relaciona de modo preciso el tamaño de la órbita de un planeta y el periodo que necesita para describir una órbita alrededor del Sol.

Cuanto más distante está el planeta, más lento es su movimiento, pero de acuerdo con una ley matemática precisa: P²=a³; donde P es el periodo de rotación alrededor del Sol medido en años, y a es la distancia que existe entre el planeta y el Sol medido en unidades astronómicas (u.a.). Así, por ejemplo, Júpiter está a 5 unidades astronómicas, por tanto: a³⁼5x5x5=125, dando como resultado un periodo de rotación P=11 aproximadamente, lo que significa que Júpiter precisa 11 años para dar una vuelta alrededor del Sol.

1 2 3 4 5

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦ Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios